혼자 만들면서 공부하는 딥러닝 3-1 MoblieNet 모델 구현 | 이미지 분류 모델의 효율성 최적화하기

서론

MobileNet은 DenseNet에서 더 진화된 CNN 모델로, 용량이 작다는 특징을 가지고 있습니다. 용량을 줄이기 위해 깊이별 합성곱 개념을 도입하였고, 이번 글에서는 이를 파이썬 코드로 구현해보고자 합니다.

 

DenseNet 구조 살펴보기

구조를 이렇게 표로 정리해보았습니다.

층	케라스 함수	내용	크기
입력층	Input()	입력	(224, 224, 3)
합성곱층	Conv2D()	필터 개수 = 32, 커널 크기 = 3, 스트라이드 = 2, 편향 사용 X, 세임 패딩	(112, 112, 32)
배치 정규화층	BatchNormalization()	입실론 크기 = 1e-5	(112, 112, 32)
렐루 활성화 함수	ReLU(max_value = 6.0)()	활성화 함수 통과	(112, 112, 32)
깊이 분리 합성곱 블록	depthwise_seperable_block()	필터 개수 = 64, 스트라이드 = 1, 제로 패딩(아래 1 오른쪽 1)	(113, 113, 64)
깊이 분리 합성곱 블록	depthwise_seperable_block()	필터 개수 = 128, 스트라이드 = 2	(56, 56, 128)
깊이 분리 합성곱 블록	depthwise_seperable_block()	필터 개수 = 128, 스트라이드 = 1, 제로 패딩(아래 1 오른쪽 1)	(57, 57, 128)
깊이 분리 합성곱 블록	depthwise_seperable_block()	필터 개수 = 256, 스트라이드 = 2	(28, 28, 256)
깊이 분리 합성곱 블록	depthwise_seperable_block()	필터 개수 = 256, 스트라이드 = 1, 제로 패딩(아래 1 오른쪽 1)	(29, 29, 256)
깊이 분리 합성곱 블록	depthwise_seperable_block()	필터 개수 = 512, 스트라이드 = 2	(14, 14, 512)
깊이 분리 합성곱 블록	depthwise_seperable_block()	필터 개수 = 512, 스트라이드 = 1	(14, 14, 512)
깊이 분리 합성곱 블록	depthwise_seperable_block()	필터 개수 = 512, 스트라이드 = 1	(14, 14, 512)
깊이 분리 합성곱 블록	depthwise_seperable_block()	필터 개수 = 512, 스트라이드 = 1	(14, 14, 512)
깊이 분리 합성곱 블록	depthwise_seperable_block()	필터 개수 = 512, 스트라이드 = 1	(14, 14, 512)
깊이 분리 합성곱 블록	depthwise_seperable_block()	필터 개수 = 512, 스트라이드 = 1	(14, 14, 512)
깊이 분리 합성곱 블록	depthwise_seperable_block()	필터 개수 = 1024, 스트라이드 = 2	(7, 7, 1024)
깊이 분리 합성곱 블록	depthwise_seperable_block()	필터 개수 = 1024, 스트라이드 = 1	(7, 7, 1024)
전역 평균 풀링	GlobalAveragePooling()	특성 맵의 차원 유지	(1, 1, 1024)
드롭아웃	Dropout()	드롭아웃 비율 = 0.001	(1, 1, 1024)
합성곱층	Conv2D()	필터 개수 = 1000, 필터 크기 = 1, 세임 패딩	(1, 1, 1000)
완전밀집층	Reshape	(1000,)	(1000, , )
활성화 함수	Activation('softmax')	각 1000개의 클래스에 대한 확률 추출	(1000, , )

 

이제 이 구조를 코드로 구현하면 아래와 같습니다.

import keras
from keras import layers

inputs = layers.Input(shape=(224, 224, 3))

x = layers.Conv2D(32, 3, padding='same', strides=2, use_bias=False)(inputs)
x = layers.BatchNormalization(epsilon=1e-5)(x)
x = layers.ReLU(max_value=6.0)(x)

for filters in (64, 128, 256):
    x = depthwise_separable_block(x, filters)
    x = depthwise_separable_block(x, filters*2, strides=2)
for _ in range(5):
    x = depthwise_separable_block(x, 512)
x = depthwise_separable_block(x, 1024, strides=2)
x = depthwise_separable_block(x, 1024)

x = layers.GlobalAveragePooling2D(keepdims=True)(x)
x = layers.Dropout(0.001)(x)
x = layers.Conv2D(1000, 1, padding='same')(x)
x = layers.Reshape((1000,))(x)
outputs = layers.Activation('softmax')(x)

model = keras.Model(inputs, outputs)

참고로 depthwise_seperable_block() 함수는 아래와 같습니다. 이는 깊이별 분리 합성곱 블록을 구현한 함수입니다.

import keras
from keras import layers

def depthwise_separable_block(inputs, filters, strides=1):
    if strides == 1:
        x = inputs
    else:
        x = layers.ZeroPadding2D(padding=((0, 1), (0, 1)))(inputs) # 위 0, 아래 1, 왼쪽 0, 오른쪽 1픽셀 추가
    # 1. 깊이별 합성곱층
    x = layers.DepthwiseConv2D(3, padding='same' if strides == 1 else 'valid',
                               strides=strides, use_bias=False)(x)

    x = layers.BatchNormalization(epsilon=1e-5)(x)
    x = layers.ReLU(max_value=6.0ㅁ)(x)
    # 2. 점곱 합성곱층
    x = layers.Conv2D(filters, 1, padding='same', use_bias=False)(x)
    x = layers.BatchNormalization(epsilon=1e-5)(x)
    x = layers.ReLU(max_value=6.0)(x)
    return x

이 모델의 summary를 보면 아래와 같습니다.

 

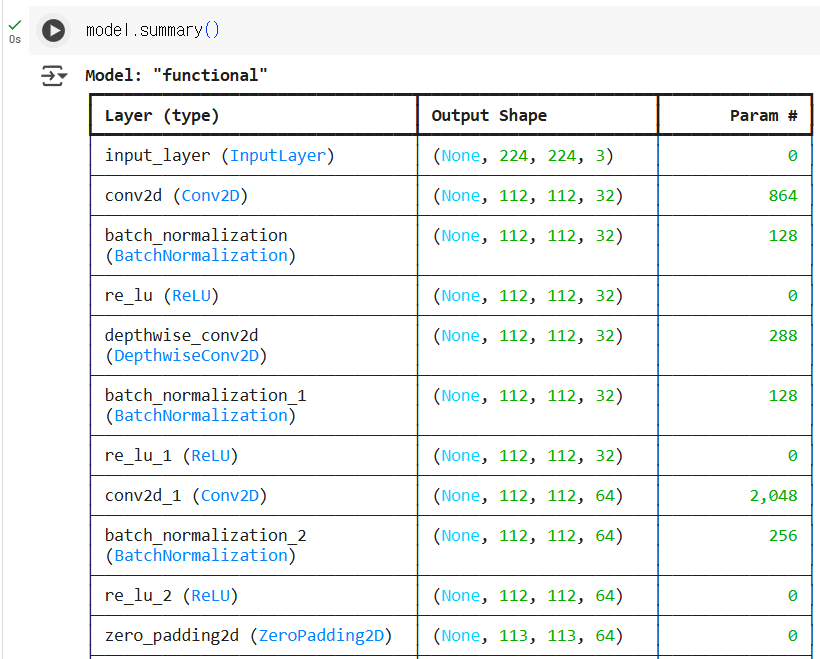
그림으로 보는 MobileNet

ⓒ 혼자 만들면서 공부하는 딥러닝 - 한빛미디어

그림으로 보면 다음과 같습니다. 처음에는 합성곱 - 배치 정규화 - 렐루 함수를 거칩니다. 그 이후 총 6개-5개-2개의 의 깊이별 분리 합성곱 블록을 거친 뒤, 전역 평균 풀링 - 드롭아웃 - 합성곱 - 크기 변경 - 소프트 맥스 함수를 거쳐 각 클래스에 대한 확률을 출력합니다.

 

MobileNet 모델로 강아지 사진 분류하기

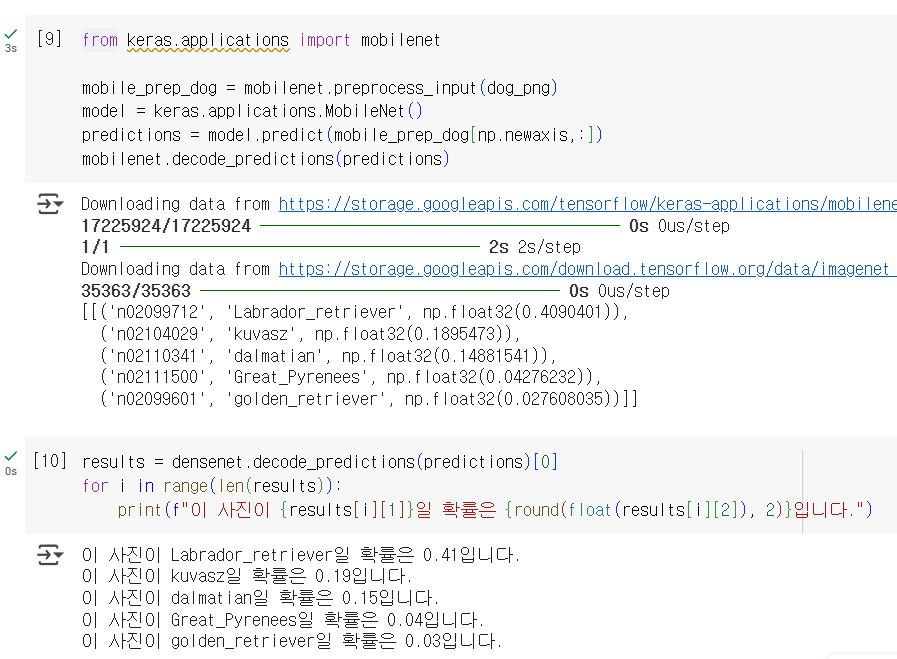
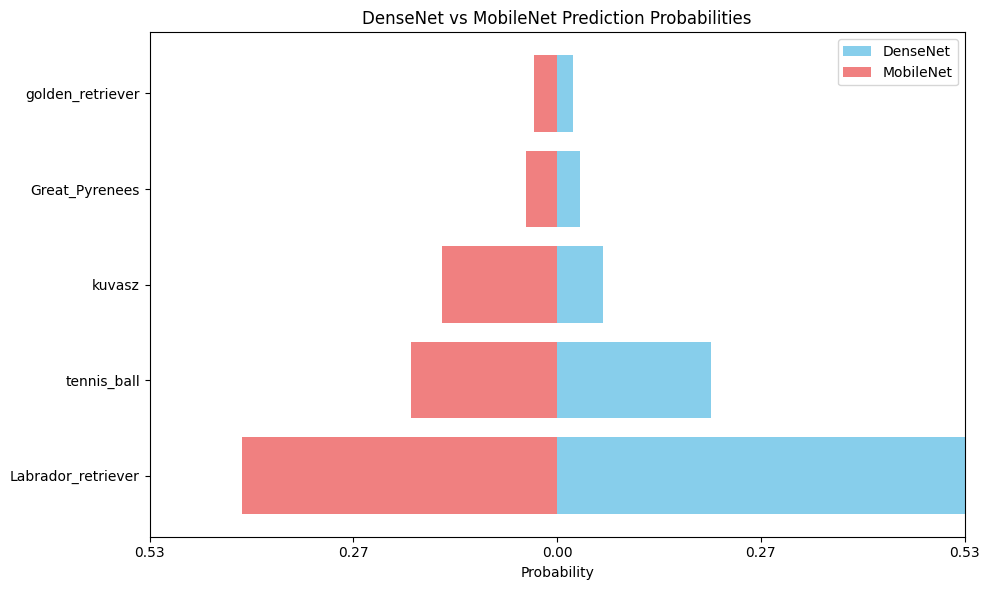
위와 같이 시각화하여 DenseNet과 MobileNet 모두 비슷한 확률로 예측하고 있음을 알 수 있습니다. Labrador retriever로 예측하는 확률이 MobileNet이 좀 더 작긴 하지만, 용량의 크기가 5배 차이남을 감안하면 MobileNet이 꽤 효율적인 모델임을 알 수 있습니다.

 

마무리

이렇게 3-1장에서는 DenseNet, MobileNet 모델의 구조에 대해서 알아보았습니다. 3-2장에서는 EfficientNet에 대해 알아볼 예정입니다.