내가 하고싶은 건 다 하는 공간
혼자 만들면서 공부하는 딥러닝 3-1 DenseNet 모델 구현 | 이미지 분류 모델의 효율성 최적화하기 본문
서론
이전 글에 이어서 DenseNet 모델에 대한 내용입니다. 이번 장에서는 케라스 클래스를 이용해서 모델을 실제로 구현합니다.
DenseNet 구조 살펴보기
구조를 이렇게 표로 정리해보았습니다.
| 층 | 케라스 함수 | 내용 | 크기 |
| 입력층 | Input() | 입력 | (224, 224, 3) |
| 패딩 | ZeroPadding2D() | 패딩 크기 = 3 | (230, 230, 3) |
| 합성곱층 | Conv2D() | 필터 개수 = 64, 커널 크기 = 7, 스트라이드 = 2, 편향 사용 X | (112, 112, 64) |
| 배치 정규화층 | BatchNormalization() | 입실론 크기 = 1e-5 | (112, 112, 64) |
| 렐루 활성화 함수 | Activation('relu')() | 활성화 함수 통과 | (112, 112, 64) |
| 패딩 | ZeroPadding2D() | 패딩 크기 = 1 | (114, 114, 64) |
| 최대 풀링 | MaxPooling2D() | 풀링 크기 = 3, 스트라이드 = 2 | (56, 56, 64) |
| 밀집 블록 | dense_block(x, blocks) | 밀집 블록 6번 반복 | (56, 56, 128) |
| 전환 블록 | transition_block(x) | 전환 블록 1개 | (28, 28, 128) |
| 밀집 블록 | dense_block(x, blocks) | 밀집 블록 12번 반복 | (28, 28, 512) |
| 전환 블록 | transition_block(x) | 전환 블록 1개 | (14, 14, 256) |
| 밀집 블록 | dense_block(x, blocks) | 밀집 블록 24번 반복 | (14, 14, 1024) |
| 전환 블록 | transition_block(x) | 전환 블록 1개 | (7, 7, 512) |
| 밀집 블록 | dense_block(x, blocks) | 밀집 블록 16번 반복 | (7, 7, 1024) |
| 배치 정규화층 | BatchNormalization() | 입실론 크기 = 1e-5 | (7, 7, 1024) |
| 렐루 활성화 함수 | Activation('relu')() | 활성화 함수 통과 | (7, 7, 1024) |
| 전역 풀링층 | GlobalAveragePooling2D() | 평균 풀링 | (1024) |
| 최종 밀집층 | Dense | 활성화 함수 = softmax | (1000) |
이제 이 구조를 코드로 구현하면 아래와 같습니다.
inputs = layers.Input(shape = (224, 224, 3))
x = layers.ZeroPadding2D(padding = 3)(inputs)
x = layers.Conv2D(filters = 64, kernel_size = 7, strides = 2, use_bias = False)(x)
x = layers.BatchNormalization(epsilon = 1e-5)(x)
x = layers.Activation('relu')(x)
x = layers.ZeroPadding2D(padding = 1)(x)
x = layers.MaxPooling2D(pool_size = 3, strides = 2)(x)
for blocks in (6, 12, 24):
x = dense_block(x, blocks)
x = transition_block(x)
x = dense_block(x, 16)
x = layers.BatchNormalization(epsilon = 1e-5)(x)
x = layers.Activation('relu')(x)
x = layers.GlobalAveragePooling2D()(x)
outputs = layers.Dense(1000, activation = 'softmax')(x)참고로 dense_block(), transition_block() 함수는 아래와 같습니다.
import keras
from keras import layers
def dense_block(x, blocks):
for _ in range(blocks):
x1 = layers.BatchNormalization()(x)
x1 = layers.Activation('relu')(x1)
x1 = layers.Conv2D(filters = 128, kernel_size = 1, use_bias = False)(x1) # 절편이 불필요. 어차피 그 다음 배치 정규화층에서 평균을 0으로 만들어버린다.
x1 = layers.BatchNormalization(epsilon = 1e-5)(x1)
x1 = layers.Activation('relu')(x1)
x1 = layers.Conv2D(filters = 32, kernel_size = 3, padding = 'same', use_bias = False)(x1)
x = layers.Concatenate()([x, x1])
return ximport keras
from keras import layers
def transition_block(x):
x = layers.BatchNormalization(epsilon=1e-5)(x)
x = layers.Activation('relu')(x)
x = layers.Conv2D(filters = int(x.shape[-1]/2), kernel_size = 1, use_bias = False)(x)
x = layers.AveragePooling2D(pool_size = 2)(x)
return x이 모델의 summary를 보면 아래와 같습니다.
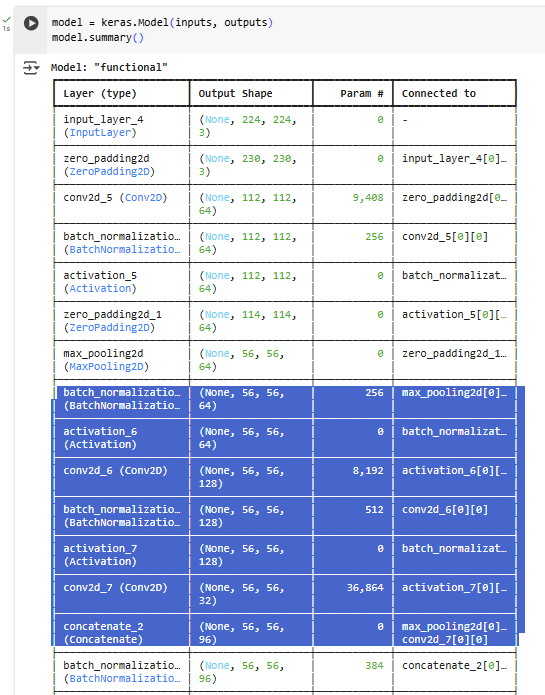
파란색으로 색칠된 부분이 하나의 밀집 블록을 나타내고 있습니다.
DenseNet 모델로 강아지 사진 분류하기
완성한 모델을 활용하여 실제로 사진을 분류해보고 성능을 확인해보겠습니다. 위에 살펴본 구조는 DenseNet-169이지만 사진 분류에서는 DenseNet-201을 사용하고 있습니다.
# 샘플 이미지 다운로드 후 압축 해제
!gdown 1xGkTT3uwYt4myj6eJJeYtdEFgTi2Sj8C
!unzip cat-dog-images.zip
# 이미지 불러오기
import numpy as np
from PIL import Image
dog_png = np.array(Image.open('images/dog.png'))
# 이미지 전처리
from keras.applications import densenet
dense_prep_dog = densenet.preprocess_input(dog_png)
# DenseNet-201로 예측 수행
densenet201 = keras.applications.DenseNet201()
predictions = densenet201.predict(dense_prep_dog[np.newaxis,:])
densenet.decode_predictions(predictions)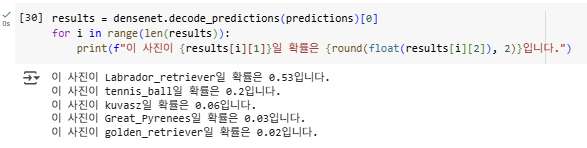
결과를 확인해보니 Labrador_retriever일 확률이 0.53이라고 합니다. 2장에서 살펴본 ResNet 모델은 Labrador_retriever일 확률이 0.39라고 응답한 것에 비해 더 강하게 예측하고 있습니다.

이 사진인데, Labrador Retriever 같나요? ㅎㅎ
마무리
이렇게 DenseNet을 직접 구현해보고, 실제 성능을 확인해보았습니다. 이 책을 계속 공부할수록 더 복잡한 모델이 나와서 공부 시간이 더 오래 걸리는 것 같습니다. ㅎㅎ 그래도 마지막까지 화이팅!
'인공지능' 카테고리의 다른 글
| 혼자 만들면서 공부하는 딥러닝 3-1 MoblieNet 모델 구현 | 이미지 분류 모델의 효율성 최적화하기 (2) | 2025.07.27 |
|---|---|
| 혼자 만들면서 공부하는 딥러닝 3-1 MoblieNet 모델, 깊이별 합성곱 | 이미지 분류 모델의 효율성 최적화하기 (1) | 2025.07.27 |
| 혼자 만들면서 공부하는 딥러닝 3-1 DenseNet 모델 준비 | 이미지 분류 모델의 효율성 최적화하기 (1) | 2025.07.27 |
| 혼자 만들면서 공부하는 딥러닝 2-3 GoogLeNet : 인셉션 모듈 Inception Module (0) | 2025.07.20 |
| 혼자 만들면서 공부하는 딥러닝 2-3 ResNet : 분류 모델 성능 개선하는 CNN 모델 (0) | 2025.07.20 |



